Liczby pierwsze – tajemnicze, fascynujące i nieodłączne od historii matematyki. Od starożytności aż po współczesne czasy, matematycy próbują rozwikłać ich zagadki, odkrywając tym samym wiele istotnych teorii i twierdzeń. W tym artykule przyjrzymy się bliżej tym unikalnym liczbom, które stanowią fundament matematyki, a także zostaną przedstawione całkiem nowe metody ich generowania oraz rozwikłamy zagadnienie o rozmieszczeniu liczb pierwszych.
Przedstawione poniżej informacje związane z użyciem dwóch prostych wzorów oraz funkcji trygonometrycznych pozwolą nam poznać zasadę jak powstają liczby pierwsze oraz przewidzieć ich bezbłędne występowanie z pominięciem jakichkolwiek działań związanych z testem pierwszości. W skrócie poznamy od dawna poszukiwany kod liczb pierwszych.
WZÓR
Poniższy wzór definiuje nieskończony ciąg liczb pierwszych bez potrzeby jakiejkolwiek faktoryzacji:
{(2), (3), (5), (6m+1), (6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0, n mod 10 ≠ 1, n mod 10 ≠ 6} \ {(6m+1)*(6n-1), (6m+1)*(6m+1), (6n-1)*(6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0 , n mod 10 ≠ 1, n mod 10 ≠ 6}
Generowanie liczb pierwszych zawsze zaczynamy od liczby 1 i dążymy do nieskończoności.
Jak zauważymy od liczb wygenerowanych ze wzorów 6m+1 i 6n-1 odejmujemy iloczyny i kwadraty liczb z tych wzorów. Iloczyny i kwadraty liczb pierwszych nazwiemy liczbami przypierwszymi (więcej informacji w dziale LICZBY PRZYPIERWSZE). Efektem usunięcia ze zbiorów 6m+1 oraz 6n-1 zbioru liczb przypierwszych jest uzyskanie bez jakiejkolwiek faktoryzacji wszystkich liczb pierwszych.
Jak powstają liczby pierwsze i przypierwsze?
Najbardziej optymalnymi wzorami na wyznaczenie dwóch ciągów liczbowych w którym pomijane jest ponad 66.66% liczb naturalnych i które wyznaczą wszystkie liczby pierwsze (oprócz liczb 2 i 3) i liczby przypierwsze są:
6n+1 oraz 6n-1 gdzie n > 0
{(6n-1), (6n+1) | n > 0}
Liczby ze zbioru 6n+1 :
7, 13, 19 ,25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127, 133, 139, 145, 151, 157, 163, 169, 175, 181, 187, 193, 199, 205, 211, 217, 223,…
Liczby ze zbioru 6n-1 :
5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95, 101, 107, 113, 119, 125, 131, 137, 143, 149, 155, 161, 167, 173, 179, 185, 191, 197, 203, 209, 215, 221,…
Mocnym argumentem jest że 50% wszystkich liczb w ciągu Fibonacciego stanowią liczby z omawianych wzorów 6n-1 oraz 6n+1, więcej informacji w dziale CIĄG FIBONACCIEGO. Liczby z omawianych wzorów tworzą również symetryczną i powtarzalną spirale, efekt można zobaczyć tutaj.
Wyznaczanie kolejnych liczb pierwszych przy pomocy funkcji trygonometrycznych.
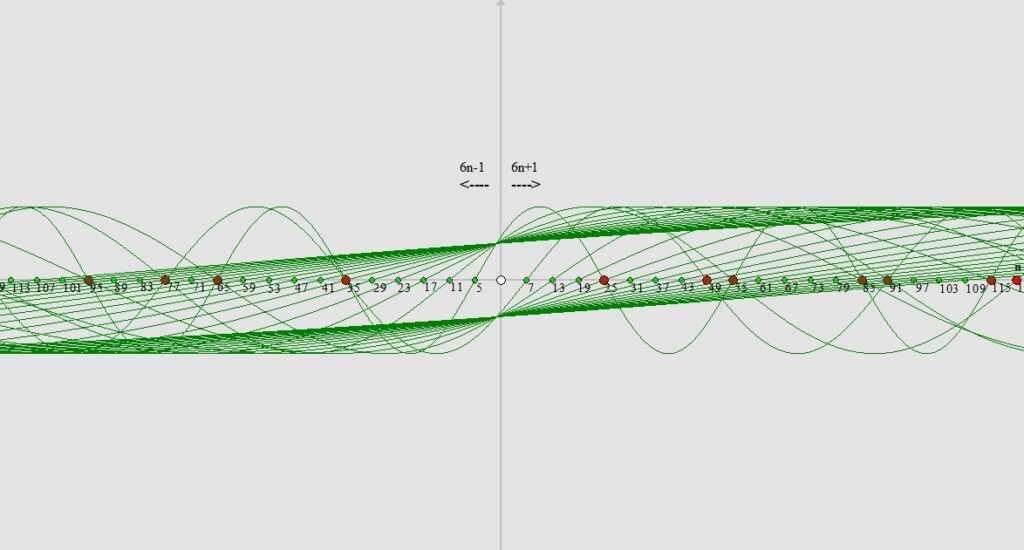
Jak widzimy na obrazku poniżej nasze dwa zbiory z liczbami pierwszymi i „przypierwszymi” umieszczamy na osi współrzędnych X. Od punktu przecięcia osi X i Y do lewej strony osadzamy liczby ze wzoru 6n-1, natomiast w prawą stronę wstawiamy liczby ze wzoru 6n+1.

Teraz z pomocą przychodzi nam odpowiednio zmodyfikowana funkcja trygonometryczna np. sinus. Wyznaczamy z naszej najmniejszej liczby, czyli z liczby „5” (oznaczonej zielonym punktem) sinusoidę która przecina oś X co 5 pozycji zarówno w prawo jak i w lewo. Na obrazku poniżej widzimy efekt tego działania:
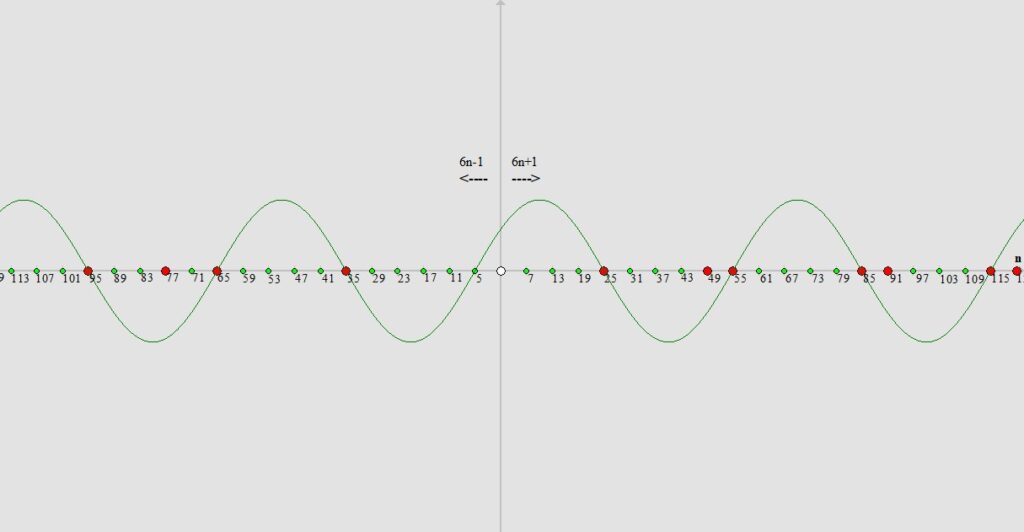
Jak widzimy powyżej miejsca w których sinusoida przecina oś X (oprócz liczby 5 bo z niej wyznaczaliśmy sinusoidę) to nasze liczby przypierwsze które nie są liczbami pierwszymi gdyż albo to kwadraty liczb pierwszych i/lub „przypierwszych” albo ich iloczyny. Jak widzimy kolejną liczbą większą od „5” to liczba „7” i z całą pewnością możemy stwierdzić jeszcze przed wyznaczeniem kolejnej sinusoidy że wszystkie liczby naturalne na naszej osi X mniejsze od wartości kwadratu liczby „7”, czyli mniejsze od „49” przez które nie przechodzi sinusoida (oprócz liczb 5 bo z niej wyznaczaliśmy sinusoidę do tej pory) są liczbami pierwszymi. Następnym krokiem będzie wyznaczenie sinusoidy która będzie przecinać oś X co siedem pozycji z liczby „7”.
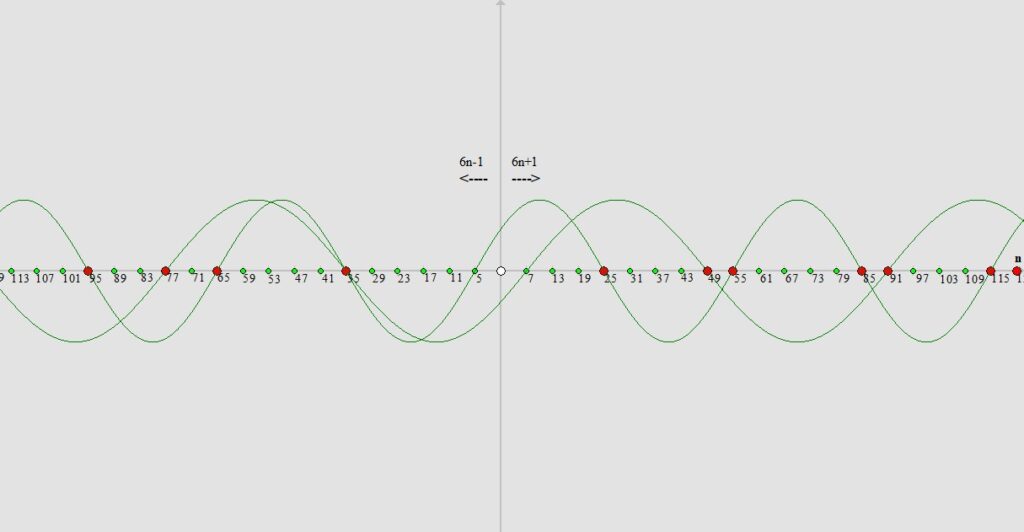
Widzimy znowu że wszystkie liczby naturalne przez które nie przechodzi żadna z wyznaczonych dotąd sinusoid (oprócz liczb 5 i 7 bo z nich wyznaczaliśmy sinusoidy do tej pory) – mniejsze od wartości „121” (czyli kwadratu następnej naszej liczby jaką jest liczba „11”) są z całą pewnością kolejnymi liczbami pierwszymi.
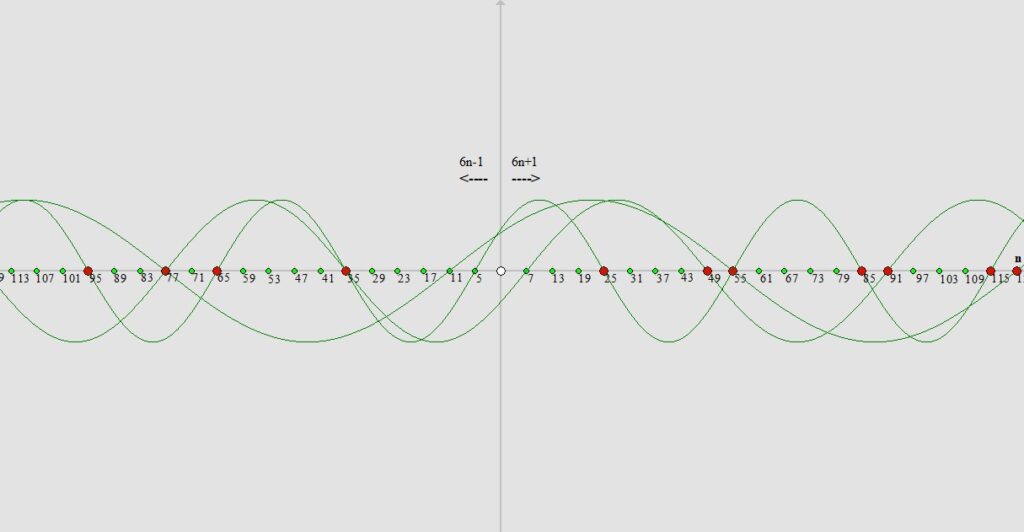
Stosując tą metodę w nieskończoność czyli z liczby „5” wyznaczając sinusoidę która przecina oś X co pięć pozycji, z liczby „7” sinusoidę przecinającą oś X co siedem pozycji, z liczby „11” sinusoidę przecinającą oś X co jedenaście pozycji itd. wyznaczamy bezbłędnie z góry liczby pierwsze mniejsze od wartości kwadratu następnej liczby z jakiej skończyliśmy wyznaczać sinusoidę.
Wszystkie liczby naturalne mniejsze od wartości kwadratu następnej liczby z jakiej skończyliśmy wyznaczać sinusoidę a zarazem większe od liczby z jakiej skończyliśmy wyznaczać sinusoidę na naszej osi X przez które przebiegła przynajmniej jedna sinusoida nie są liczbami pierwszymi (oczywiście oprócz liczb z których wyznaczaliśmy sinusoidę). Należy pamiętać by wyznaczać sinusoidę stopniowo czyli wpierw z liczby „5” później „7”, „11”, „13”,”…”.
Niektórzy zapewne stwierdzą że to zmodyfikowane sito Eratostenesa, jednak nie ma takiego sita które jeszcze przed sprawdzeniem danej liczby (a w zasadzie ciągu liczb) definiowałoby bezbłędnie kolejne liczby pierwsze mniejsze od wartości kwadratu tej liczby w zbiorze jaki mielibyśmy sprawdzać.
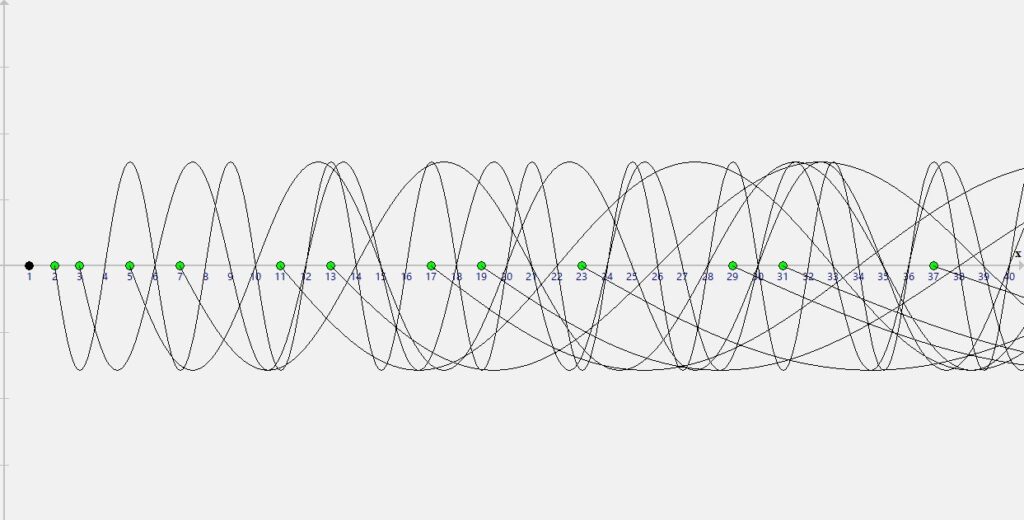
Można użyć metody która zawiera wszystkie liczby naturalne do wyznaczania kolejnych liczb pierwszych gdzie tak samo będzie sprawdzała się zasada że po wyznaczeniu sinusoidy z konkretnej liczby, wszystkie liczby mniejsze od kwadratu następnej liczby naturalnej przez którą nie przebiega sinusoida są liczbami pierwszymi, jednak metoda ta zmusza nas do operacji na wszystkich liczbach naturalnych co widać na obrazku poniżej;
HIPOTEZY
Kod liczb pierwszych i to, w jaki sposób one powstają, został poznany dzięki funkcjom trygonometrycznym (w zasadzie mnożeniu). Operacje te są znacznie efektywniejsze obliczeniowo dla komputerów niż skomplikowane działania matematyczne, takie jak faktoryzacja liczb pierwszych i dzielenie. Co więcej, zastosowanie wzorów 6n-1 oraz 6n+1 ogranicza poszukiwanie liczb pierwszych do zaledwie 26,66% wszystkich liczb naturalnych (przy założeniu eliminacji z naszego zbioru liczb większych od 5, które są zakończone cyfrą 5).
Warto zwrócić uwagę, że wszystkie kwadraty liczb ze zbiorów 6n+1 oraz 6n-1 zawsze występują wyłącznie w zbiorze 6n+1. Ponadto iloczyn dwóch liczb należących do tego samego zbioru (6n+1 lub 6n-1) znajduje się tylko zbiorze 6n+1. Suma cyfr liczby należącej do zbioru 6n+1 wynosi zawsze 1, 4 lub 7.
Zbiór 6n-1 zawiera więcej liczb pierwszych, gdyż dodatkowo znajdują się w nim jedynie iloczyny liczb, w których jednym czynnikiem jest liczba ze zbioru 6n-1, drugim liczba ze zbioru 6n+1. Suma cyfr liczby należącej do zbioru 6n-1 wynosi natomiast 2, 5 lub 8.
Każdą liczbę o sumie cyfr 2, 5 lub 8 czyli należącą do zbioru 6n-1 żeby sprawdzić czy jest liczbą pierwszą wystarczy dzielić tylko przez liczby ze zbioru 6n-1 lub 6n+1, które są mniejsze od pierwiastka sprawdzanej liczby, co powoduje przyśpieszenie uzyskania odpowiedzi czy jest liczbą pierwszą.
Liczba pierwsza lub przypierwsza (z wyjątkiem liczby 3) nigdy nie będzie miała sumy cyfr 3, 6 i 9.
Przypomnę, że Nikola Tesla uważał liczby 3, 6 i 9 za wyjątkowe.
Warto zwrócić uwagę że liczby przypierwsze tworzą wartość wykładnika n klucza publicznego w algorytmie szyfrowania RSA. Więcej informacji w dziale RSA.
Ten artykuł jest dostępny także w języku angielskim, kliknij tutaj.